How to Use Pagerank as a Filter

Making binary decisions—who to serve, who to ignore, who gets access—is a recurring challenge in decentralized networks like Nostr. Whether you’re trying to block spam, prioritize trustworthy users, or reward top creators, you need a way to filter based on reputation.

Traditional methods like whitelists or blacklists don’t scale well. But reputation algorithms like Pagerank, originally developed by Google to rank web pages, offer a powerful and automated approach. By analyzing the social graph, Pagerank assigns a rank to each user, giving you a powerful and actionable signal for filtering.

In this article, we’ll explore how Pagerank works, how to set thresholds to suit your use case, and how this model can power everything from spam prevention to premium access and targeted rewards.

The How

The easiest way to try this in practice is through the use of specialized NIP-90 data vending machines. At Vertex, we offer several services that follow a consistent pattern: you receive pubkey and its associated rank, which was computed from the sort parameter you specify. Here is a sample response that uses sort=globalPagerank:

[
	{
		"pubkey": "726a1...a1c11",
		"rank": 00016816930295038342
	},
	{
		"pubkey": "f683e...f5ef2",
		"rank": 0.00008207271004088555
	},
	{
		"pubkey": "d5ad3...09387",
		"rank": 0
	},
]

The next step is turning these ranks into a simple binary decision: should you serve this pubkey or not?

A simple and effective approach is to apply a threshold. You treat a pubkey as reputable if and only if its rank exceeds that threshold. So the real challenge becomes: how do you choose a threshold that makes sense?

Pagerank

Before we can choose a threshold, it helps to understand the basics of Pagerank.

A graph $G$ consists of vertices $V$ and edges $E$. Vertices represent entities (in this case, pubkeys), and edges represent relationships (e.g., follows).

Pagerank is a function $\pi_G$ that assigns a score to each vertex: we write $\pi_G(v)$ to indicate the pagerank of vertex $v$.

Both global and personalized Pageranks have the following properties:

1. All ranks are non-negative: $\pi_G(v) \geq 0$
2. The ranks always sum to 1: $\sum_{v \in V} \pi_G(v) = 1$

Thanks to the second property, we can easily compute the average pagerank in the graph $G$ by summing all the scores and dividing by $N$, the number of vertices.

Multiples of this base quantity $1/N$ are good candidates for the threshold $T$. That said, that there is no silver bullet for choosing it—you have to decide based on your use case. Higher thresholds are more exclusive, which means they reduce spam but increase the risk of filtering out honest users.

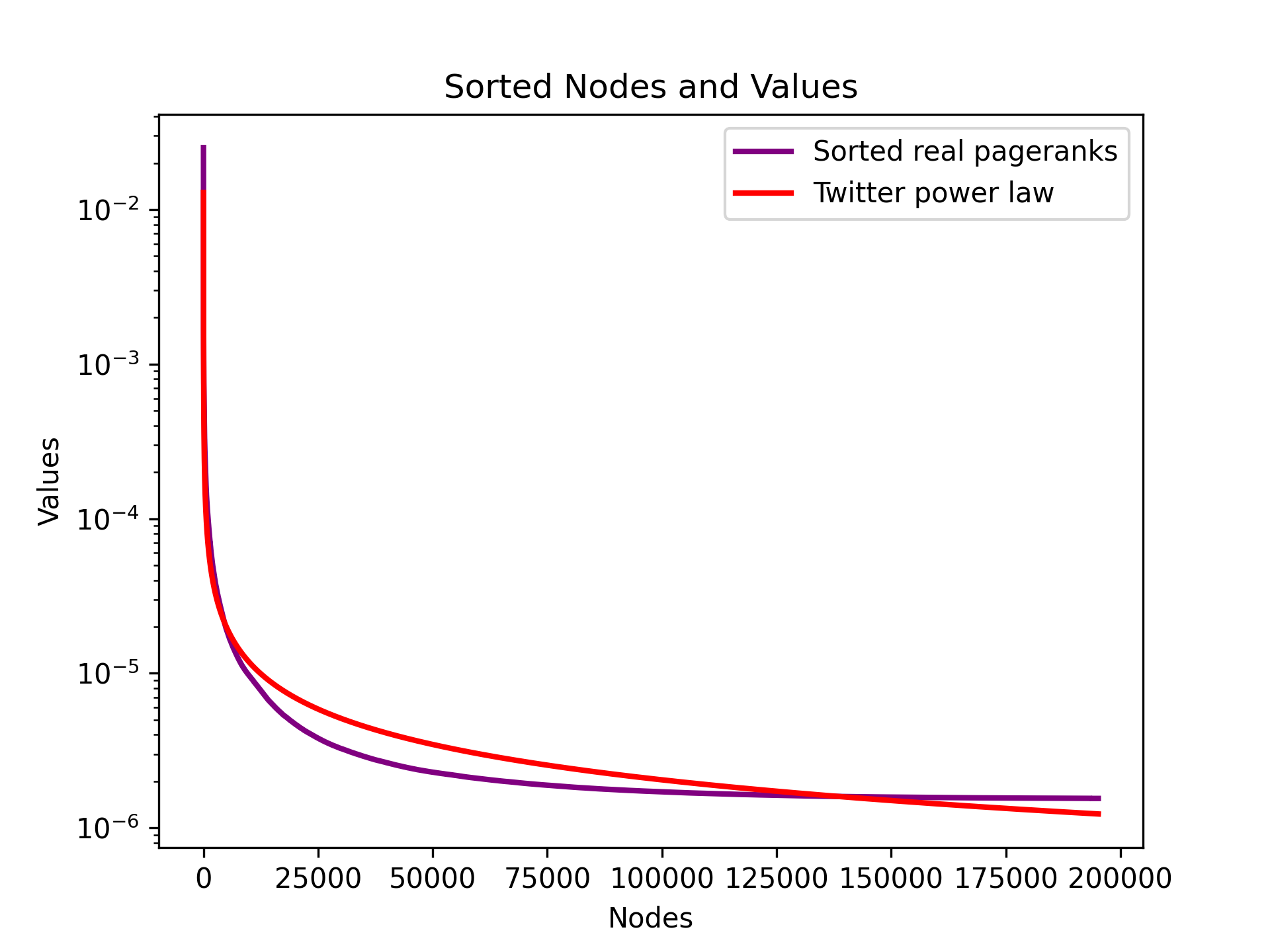
There’s one more useful property to help guide the choice of $T$. Research [1,2] shows that pagerank scores in social graphs follow a power law, meaning a small number of vertices have high ranks, while the ranks drop sharply for the rest.

Let $\pi_j$ be the the $j$-th highest pagerank value in the graph. Empirical data (Twitter, b=0.76 (2010)) shows that:

By working out the math, one can estimate the constant of the power law, which turns out to be

The following figure shows how good this model still is, 14 years later, applied to Nostr (May 2024, $b=0.76$).

Now comes the practical part. Suppose you only want to block access to the bottom 10% of the network. You can simply plug $j=0.9 \cdot N$ into the formula to get the threshold

If you want to allow access only to the top 1% of the network (e.g., for a premium community), the threshold becomes:

More generally, if you want to include only the top $x$ portion of the network (with $0 < x < 1$):

Keep in mind that there’s no one-size-fits-all threshold—it all depends on your use case, and the value of $N$ (which is currently 315k for our database). As a rule of thumb, the higher the threshold, the stricter the filter, which increases the risk of excluding legitimate users along with spam.

For example, at Vertex we currently use this value for one of our internal filters:

This alone filtered out the vast majority of spam from our database. For context, while nostr.band tracks over 40 million pubkeys, our filtered set contains only 315,000—a +100x reduction.

Sources

[1] N. Litvak, W. R. W. Scheinhardt, and Y. Volkovich. In-degree and PageRank: Why do they follow similar power laws?

[2] B. Bahmani, A. Chowdhury, and A. Goel. Fast Incremental and Personalized